首先来介绍灰度共生矩阵的公式,这是最重要也是最基本的。
Fig.1 GLCM 计算公式
其中,W为滑动窗口的大小,Moving step为滑动窗口移动的距离,而d为共生距离,也就是灰度共生矩阵中的d,最后的K为量化后的灰度级别。
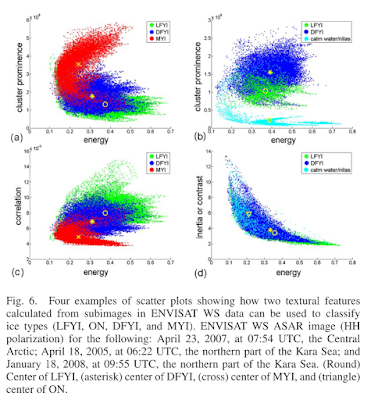
每一个窗口均获得一个GLCM,然后依据这些GLCM可以获得特征参数,然后即可获得如Fig.4 的散点关系图。
注意
Fig.1 GLCM 计算公式
Fig. 2 GLCM计算参数实验
Fig.3 滑动窗口的理解
Note: Fig.3 所示为水平方向(0度)获得共生矩阵的演示图。其他3个方向(45度、90度和135度)情况类似。
每一个窗口均获得一个GLCM,然后依据这些GLCM可以获得特征参数,然后即可获得如Fig.4 的散点关系图。
Fig.4 不同纹理特征的散点图
注意
需要注意的一点是,如果选定4个方向为GLCM的计算方向,那么在根据GLCM计算纹理特征时,需要首先根据4个方向的GLCM计算其纹理特征,然而将这4个方向的纹理特征取平均,获得最终的纹理特征计算结果[1]。
Reference: